A cadeia cinemática dos braços robóticos eezyBotArm, adoptada dos robots manipuladores industriais ABB-IRB460, é baseada em três actuadores, uma base rotativa e duas hastes em T. Uma das quais controlada directamente e outra de forma indirecta. A este sistema principal de duas hastes, está associado um outro sistema de hastes (no modelo 3D mais abaixo estão a roxo) cujo propósito é garantir a horizontalidade da aplicação da garra.
Todos os robots que seguem este modelo tem uma cadeia cinemática semelhante e todas as descrições, fórmulas, e cálculos aqui apresentados, que foram efectuados com base no eezyBotArm MK2, com uma escala de 7 para 1 face ao ABB-IRB460, aplicam-se a outros braços robóticos, como o eezyBotArm MK1 e o eezyBotArm MK3, com as devidas adequações nos parâmetros usados.
Acção dos actuadores nos braços robóticos eezyBotArm
Um actuador colocado na base e que roda o suporte das hastes segundo o eixo do z (vertical com o plano) e controla o posicionamento da garra no eixo do y, conforme video abaixo.
Um actuador que está acoplado ao braço principal, a azul no video, cujo eixo de rotação se encontra na sua extremidade inferior e controla o posicionamento da garra no eixo do x dentro de uma trajectória inscrita na circunferência do seu raio, conforme video abaixo.
Um ultimo actuador está acoplado indirectamente, por meio de duas hastes intermédias, à extremidade traseira do braço horizontal, a vermelho no video, que roda sobre o eixo na extremidade superior do braço principal e controla o posicionamento da garra no eixo do z dentro de uma trajectória inscrita na circunferência do seu raio, conforme video abaixo.
Esta haste horizontal é actuada por intermédio de duas outras hastes, a verde na imagem abaixo, que conduzem o movimento do servo.
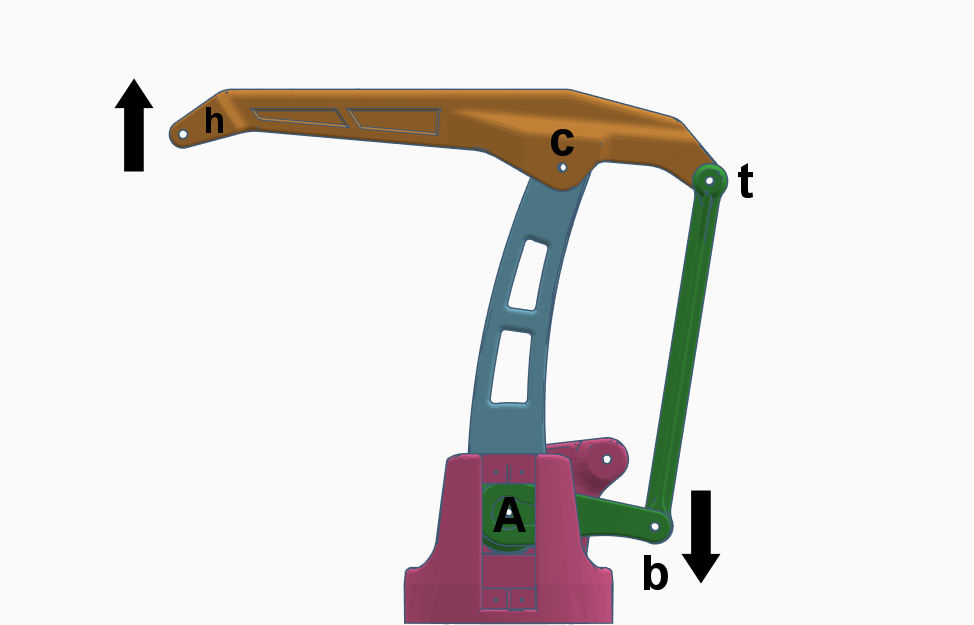
Quando o actuador na haste A, roda para baixo (no caso de um servo quando o ângulo se move para zero), conjunto das hastes verdes desce, puxando para baixo a parte de traz da haste horizontal (ponto t), que devido ao seu eixo de rotação (ponto c), faz subir a sua parte da frente (ponto h).
Os movimentos da haste principal, a azul, em torno do ponto A e da haste horizontal, a amarelo, em torno do ponto c definem a posição do ponto h face aos eixos x e z, ou seja a distancia da projecção de de h para A, e a altura do ponto h.
A amplitude dos movimentos deste tipo de robots está condicionado pela amplitude de rotação dos motores, das engrenagens que eventualmente estejam envolvidas e das colisões que se possam verificar.
No caso do braço robóticos eezyBotArm MK2, os limites são impostos pelos:
- Servos de 180º de amplitude de rotação;
- Carretos envolvidos na rotação sobre o eixo z, um principal (movido pelo servo 0) com 25 dentes e o segundo com 50 dentes, o que faz com que o movimento de rotação sobre esse eixo tenha apenas 90º de amplitude;
- Colisões entre a haste horizontal (servo 2) e a haste principal (servo 1) que implica que os servos que as movimentam têm respectivamente os seguintes limites: 60º entre os 45º e os 105º (servo 2), e 90º entre os 55º e os 145º (servo 1).
Cálculo da cinemática inversa no eezyBotArm
A cinemática inversa refere-se ao cálculo dos ângulos adequados aos diversos eixos accionados por actuadores de modo a que o ponto de acção do braço (end effector) se posicione num ponto especifico do espaço.
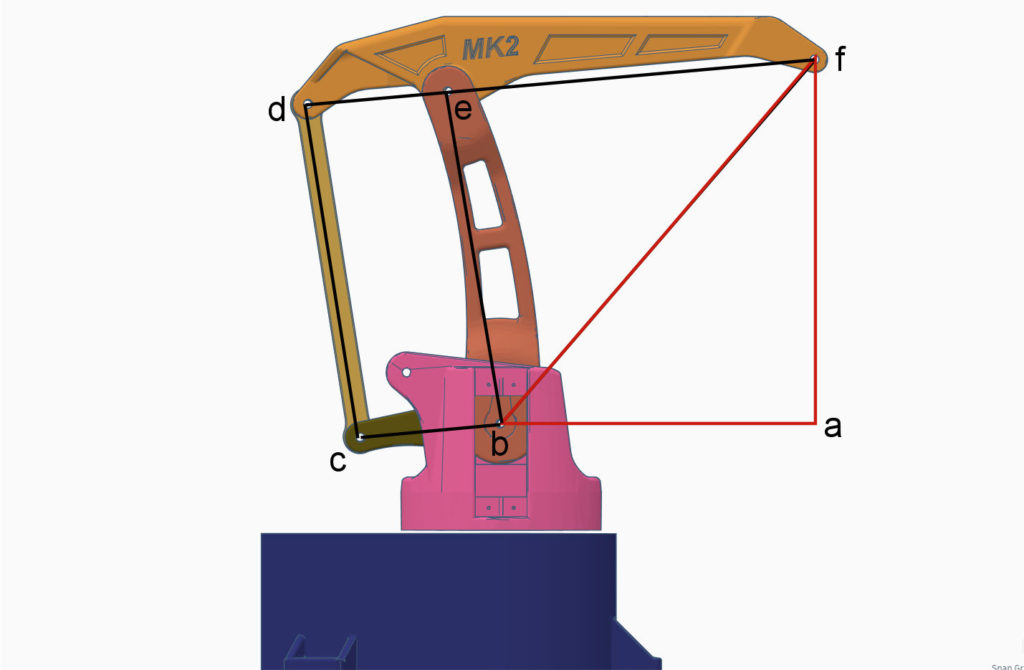
Dado um determinado ponto a (ver figura mais abaixo) com as coordenadas x, y e z relativamente à origem que para facilitar consideramos estar no centro de rotação do robot a uma altura L (no eixo dos z), o calculo da cinemática inversa envolve a conversão das coordenadas cartesianas, desse ponto, em coordenadas cilíndricas e a partir delas extrair o ângulo desejado para cada um dos três actuadores.
https://pt.wikipedia.org/wiki/Coordenadas_cil%C3%ADndricas
Os cálculos são efectuados nas seguintes fases.
Primeira fase. Conversão das coordenadas cartesianas em coordenadas cilíndricas.
Nestas coordenadas, o ângulo theta é expresso em radiano e o z mantém-se cartesiano. Por isso temos:
- theta = atan(y/x)
- raio = srt(x*x + y*y)
- z = z
O theta é o ângulo que se relacionada com o motor 0, e define a rotação em torno do eixo dos z, que antes de ser transformado em graus para ser aplicado ao motor sofre a seguinte alteração:
Ângulo do motor 0 = 2 * theta + pi / 2
Numa segunda e terceira fases, efectuam-se os cálculos dos outros dois motores, que me conjunto são responsáveis pelo posicionamento nos eixos do x e do y.
Para calcular os ângulos teremos que considerar a aplicação da lei dos cossenos.
https://pt.wikipedia.org/wiki/Lei_dos_cossenos
Consideremos o terceiro caso:
c*c = a*a + b*b – 2 * a * b * cos C
Resolvemos em ordem a cos C
c*c = a*a + b*b – 2 * a * b * cos C é equivalente a
0 = a*a + b*b – c*c – 2 * a * b * cos C é equivalente a
2 * a * b * cos C = a*a + b*b – c*c é equivalente a
cos C = (a*a + b*b – c*c) / (2 * a * b) é equivalente a
ângulo C = acos((a*a + b*b – c*c) / (2 * a * b)) a
Com base na definição de pontos expressa na imagem anterior, consideremos na aplicação da formula acima e na seguinte que:
a = L2 = distancia entre os pontos be, b = sqrt(), e c = L3 = distancia entre os pontos ef
Ângulo do motor M1 = atan(z / raio) + leicossenos(L2, sqrt(raio*raio + z*z), L3)
Pela aplicação
Ângulo do motor M2 = pi – (M1 + leicossenos(L2, L3, sqrt(raio*raio + z*z)) – pi/2)
Os ângulos calculados acima estão expresso em radiano. Antes de serem aplicados aos motores tem de ser convertidos em graus.
Abaixo segue o bloco de código em python que calcula a cinemática inversa nos braços eezyBotArm
L1 = 94
L2 = 150
L3 = 150
#Hipotenusa:
def hipo(x,y):
return math.sqrt(x*x + y*y)
#Cosines law:
def lawOfCosines(a,b,c):
rate = (a*a + b*b - c*c) / (2 * a * b)
if abs(rate) > 1:
if max(rate,0) == 0:
rate = -1
if max(rate,0) == rate:
rate = 1
return math.acos(rate)
def deg(rad):
return rad * 180 / math.pi
# Posição em coordenadas cartesianas
cartP = {'xEE': x, 'yEE': y, 'zEE': z}
# Posição em coordenadas cilindricas
cylP = {'theta': math.atan(cartP['yEE']/cartP['xEE']), 'r':hipo(cartP['xEE'], cartP['yEE']), 'zhat':cartP['zEE']-L1}
zhat = cylP['zhat']
rho = hipo(cylP['r'], zhat)
# Ângulos calculados em radiano
M1 = 2*cylP['theta'] + math.pi/2
M2 = math.atan(zhat/cylP['r']) + lawOfCosines(L2,rho,L3)
M3 = M2 + lawOfCosines(L2,L3,rho) - math.pi/2
# Ajustes
angles = [M1,math.pi - M2,M3]
# Conversão dos angulos para graus
angles = [deg(angle) for angle in angles]
Cálculo da cinemática directa no eezyBotArm
A cinemática directa refere-se ao do ponto especifico no espaço onde se posiciona elemento de acção do braço (end effector), dados os ângulos adequados aos diversos eixos accionados por actuadores.
Neste caso, os cálculos não o inverso do aplicado acima, e passam por determinar as coordenadas cartesianas em função do calculo da coordenada cilíndrica tendo em conta os angulos dos actuadores e os parâmetros físicos do braço.
Abaixo segue o bloco de código em python que calcula a cinemática directa nos braços eezyBotArm
L1 = distancia entre o ponto b e a superfície onde assenta o braço, L2 = distancia entre os pontos be, L3 = distancia entre os pontos ef.
# conversão dos angulos para radianos: angles = [joint*math.pi/180 for joint in joints.data] # cálculo intermédio para a conversão para as coordenadas cartesianas r = L2*math.cos(math.pi - angles[1]) + L3*math.cos(angles[2]-math.pi/2) # Posição do ponto expresso em coordenadas cartesianas: x = r*math.cos((angles[0]-math.pi/2)/2) y = r*math.sin((angles[0]-math.pi/2)/2) z = L2*math.sin(math.pi - angles[1]) + L3*math.sin(angles[2]-math.pi/2) + L
Folha de cálculo para a cinemática directa:
https://docs.google.com/spreadsheets/d/1DB-M-31lVDcXrwiRjAp6iKgvtpz-O-wC2fAOD7AwXrc/edit?usp=sharing
Fontes
https://github.com/HotBlackRobotics/ntbd
https://hackaday.io/project/157951
https://github.com/IdreesInc/EEZYbotARM-MK2-Cartesian-Coordinates