Este artigo descreve as duas experiências no âmbito da visão artificial efectuadas numa simulação no gazebo com recurso ao método warpPerspective em python
Em python o método warpPerspective permite calcular como uma imagem seria vista de outra perspectiva.
dst = cv2.warpPerspective(src, transform_mat, dsize[, dst[, flags[, borderMode[, borderValue]]]] )
src: imagem original
transform_mat: matriz da transformação
dsize: tamanho da imagem gerada (w,h)
flags: (opcional) métodos de interpolação
A matriz da transformação é o ponto essencial sendo composta pelos elementos descritos na seguinte imagem.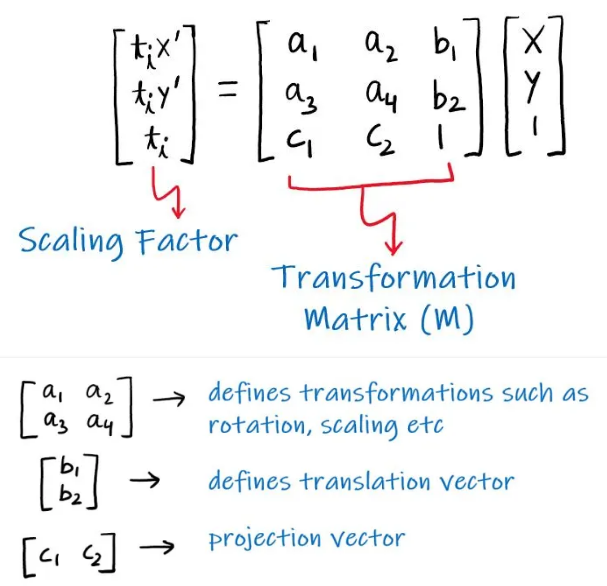
O principal problema na aplicação deste método é a obtenção da matriz da transformação.
Para isso existem dois métodos no python, em ambos os casos são necessárias as coordenadas de 4 pontos, na imagem de origem e na imagem de destino.
- transform_mat , status = cv2.findHomography(pts_src, pts_dst)
- transform_mat = cv2.getPerspectiveTransform(pts_src, pts_dst)
# pts_src: coordenadas de 4 pontos na imagem original
# pts_dst: coordenadas desses 4 pontos na imagem transformada
No caso desta abordagem para obter a vista superior (bird eye view) pelo método IPM, usaremos apenas o método getPerspectiveTransform.
Para descobrir as novas coordenadas dos quatro pontos foram colocadas em prática duas experiências no Gazebo.
Nestas experiências foi usado um programa de manipulação de perspectiva de modo a facilitar o calculo dos pontos. No entanto, o processo pode ser efectuado sem a ele se recorrer.
Experiência sem manter proporções
Foi montando o seguinte ambiente no gazebo. Um objecto rectangular e plano, de espessura desprezível, foi colocado à frente de uma viatura equipada com uma camera, de modo a ocupar todo o campo de imagem longitudinal.

imagem 1
Note-se que a quadricula tem 25 cm de lado, e que o centro da viatura e o centro da zona cinzenta estão sobre o mesmo eixo. A zona cinzenta tem 50 cm de largura. A imagem da camera existente da viatura, visualizada com o image view, é a seguinte.

imagem 2
Visualização com o programa de transformação, onde se constata que para os parâmetros exibidos a imagem é igual.
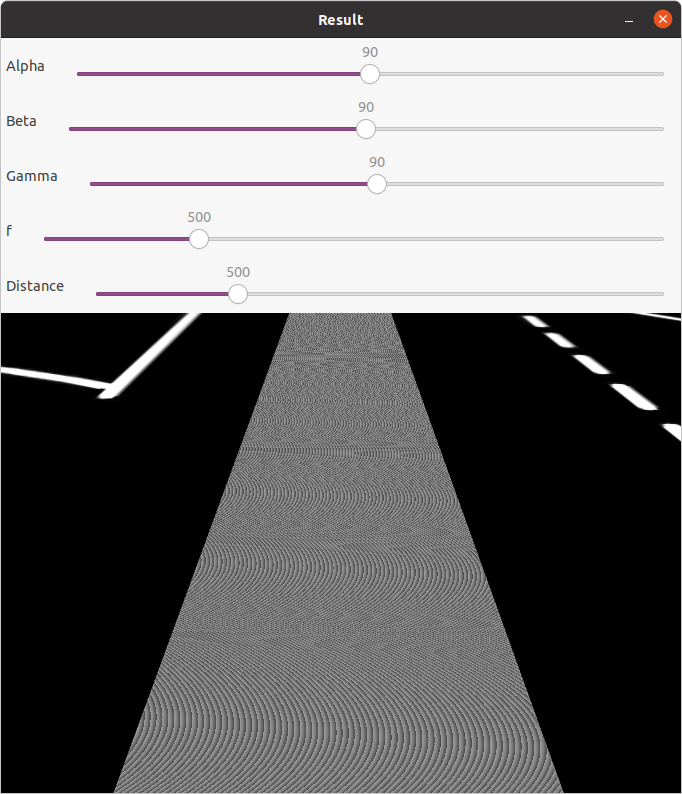
imagem 3
Visualização com o mesmo programa alterando apenas o parâmetro correspondente ao pitch
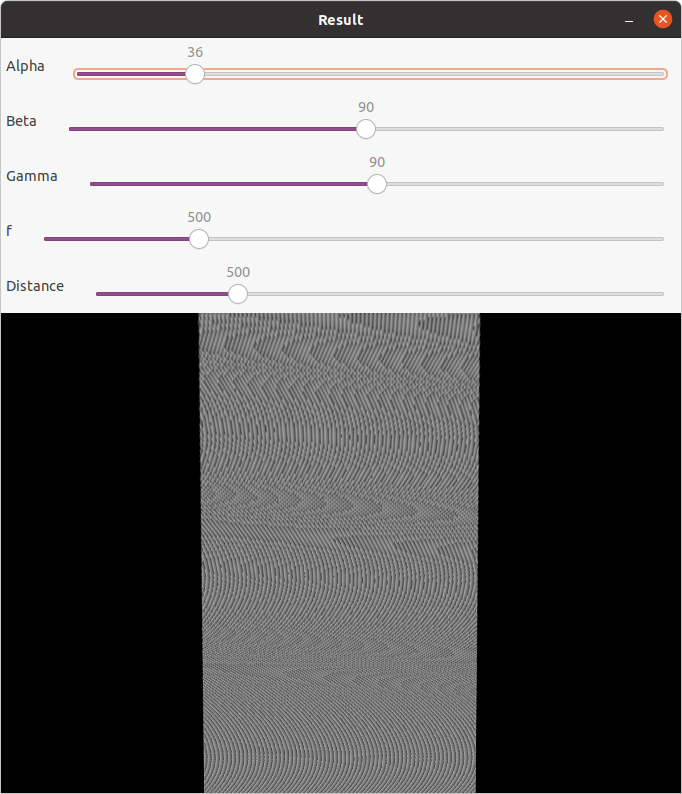
imagem 4
Com base na imagem 2 foram seleccionados os pontos dos 4 vertices do trapézio cinzento. Que têm as seguintes coordenadas, no sentido dos ponteiros do relógio, iniciando no topo superior esquerdo:
[200,0], [478,0], [200,479], [478,479]
Com base na imagem 4 foram seleccionados, os 4 pontos de correspondentes na imagem transformada.
[288, 0], [391, 0], [113, 479], [563, 479]
Estes pontos foram inseridos no seguinte programa (programa1), que quando executado, e conforme esperado, produziu uma imagem semelhante à da imagem 4.
import cv2
import numpy as np
img = cv2.imread('image2.jpg')
# define points coordinates
dst_pts = np.array([[200,0], [478,0], [200,479], [478,479]], dtype=np.float32)
src_pts = np.array([[288, 0], [391, 0], [113, 479], [563, 479]], dtype=np.float32)
# compute IPM matrix and apply it
transform_matrix = cv2.getPerspectiveTransform(src_pts, dst_pts)
ipm = cv2.warpPerspective(img, transform_matrix, img.shape[:2][::-1], flags=cv2.INTER_CUBIC)
# display image
cv2.imshow('ipm', ipm)
cv2.waitKey()
De seguida, aplicamos exactamente a mesma transformação à seguinte imagem.

image 5
O resultado da transformação obtida é o seguinte:

imagem 6
Nesta imagem (6) verifica-se a compressão da distância que acontece na altura da imagem. Isto acontece porque, para o mesmo campo angular de visão, o deslocamento ao longo dos 45º de arco de circunferência, de A1 para A2, provoca a aproximação do ponto a a b, até serem coincidentes.
Esta situação está ilustrada na imagem seguinte.
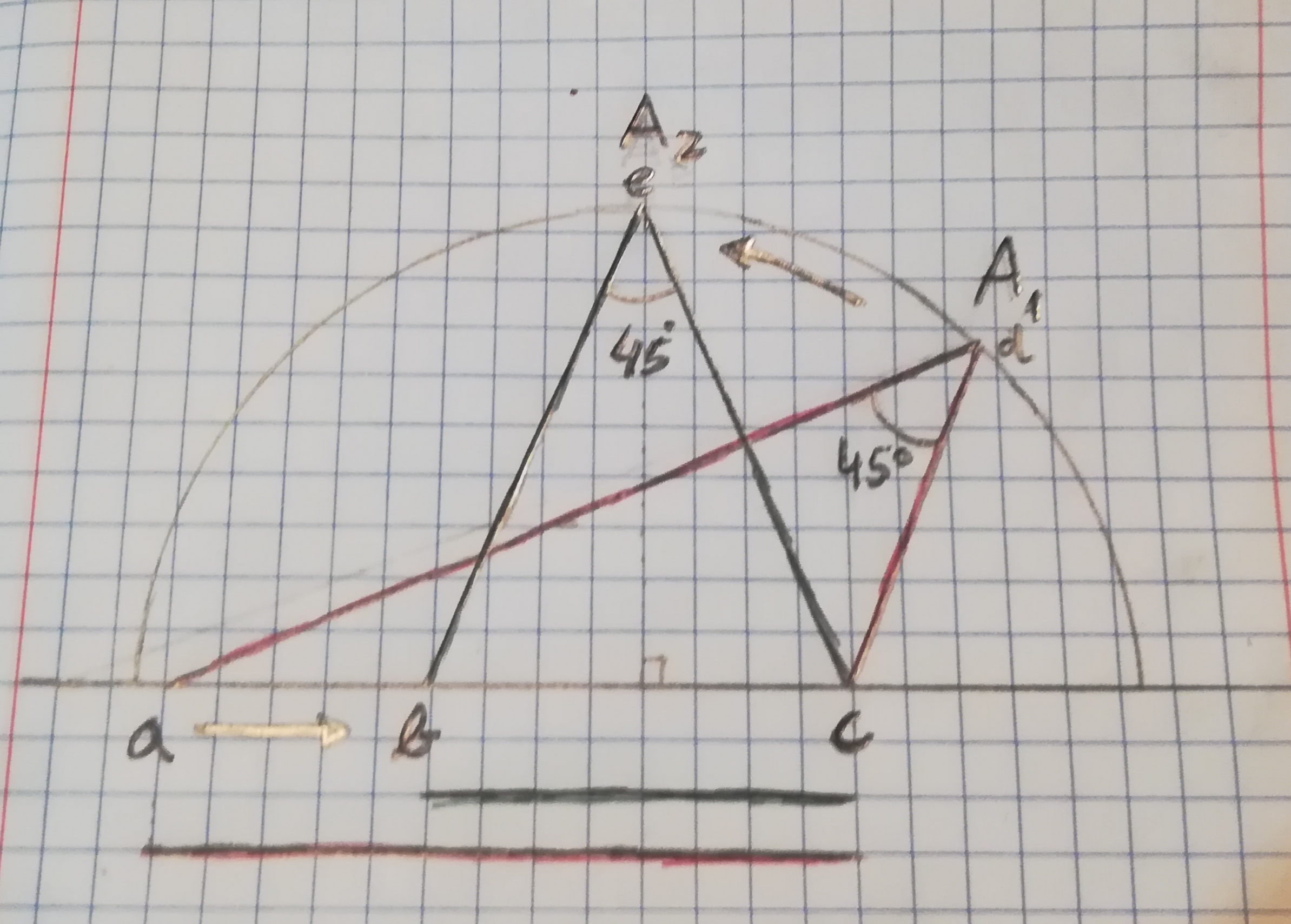
imagem 7
Experiência mantendo as proporções
Foi montando o seguinte ambiente no gazebo. Um objecto quadrado e plano, com 1 m de aresta e de espessura desprezível, foi colocado à frente de uma viatura equipada com uma camera.
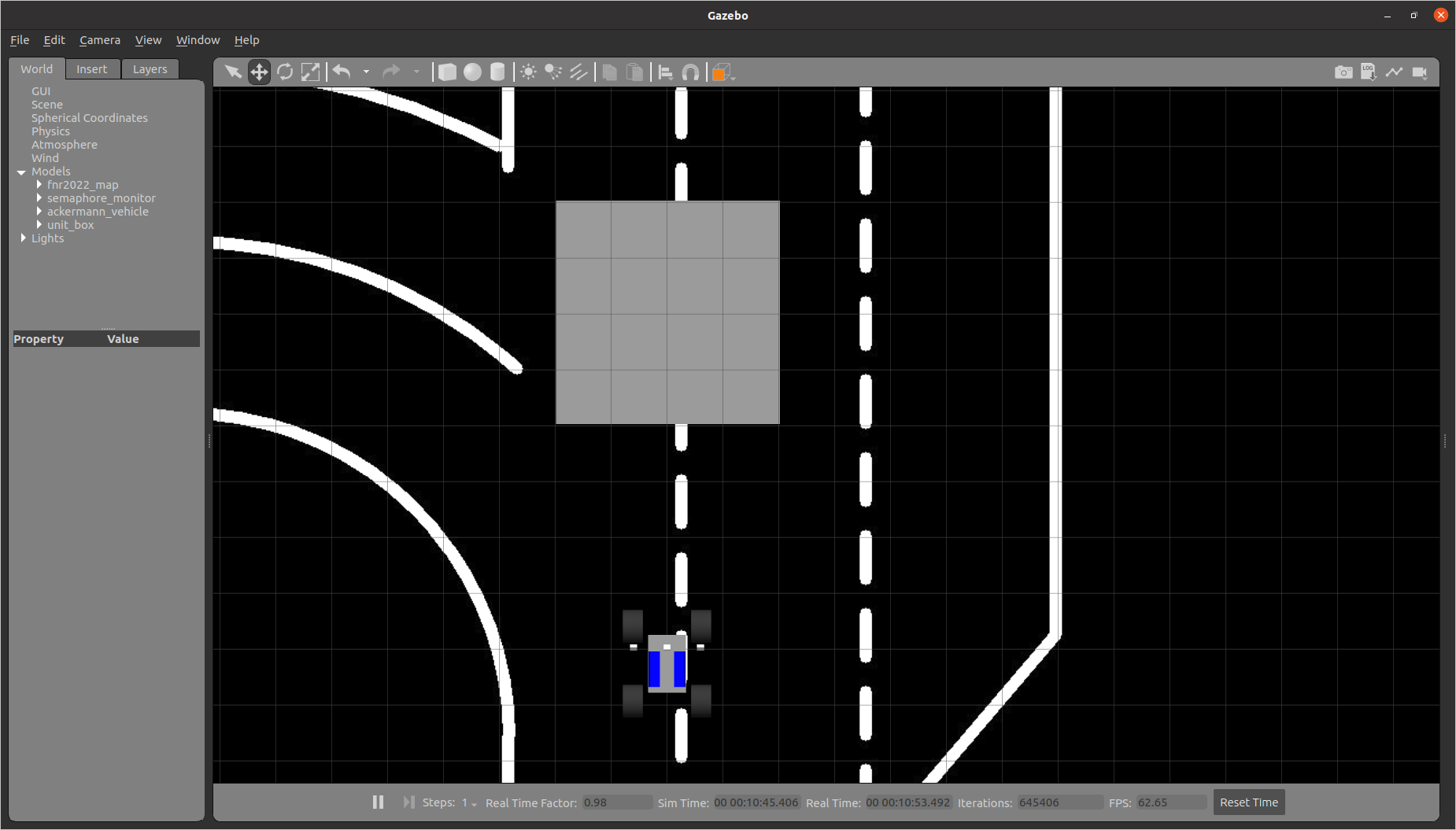
imagem 8
A aresta mais próxima do quadrado, dista 1 metro da projecção vertical da camera sobre a estrada.
A quadricula tem 25 cm de lado, e que o centro da viatura e o centro da zona cinzenta estão sobre o mesmo eixo.
Neste caso a imagem da camera existente da viatura, visualizada com o image view, é a seguinte.

imagem 9
Desta vez omitimos a exibição da imagem no programa de transformação, já que se sabe ser igual a imagem 9.
Quando se aplica um pitch de 37º (à pouco foi usado 36) o aspecto da imagem transformada fica o seguinte.
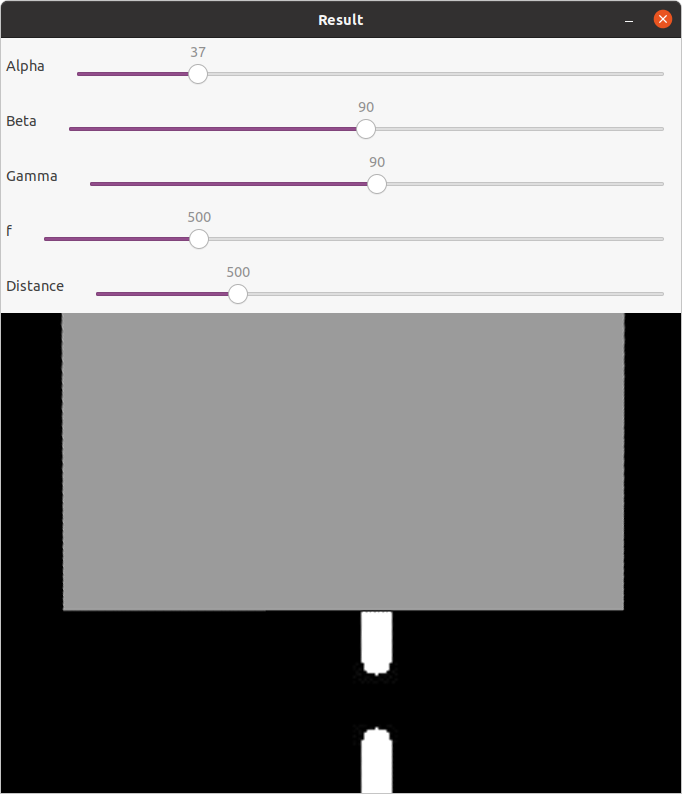
imagem 10
Neste programa de transformação não acontece o efeito de compressão, o efeito da compressão resultou da escolha, na experiência anterior de transformar os pontos apenas quanto à componente transversal da coordenadas, mantendo as coordenadas longitudinais iguais.
No entanto, o quadrado não aparece todo visível, pelo que se torna necessário ajustar a distancia do quadrado ao carro de modo a que se consiga ver todo.
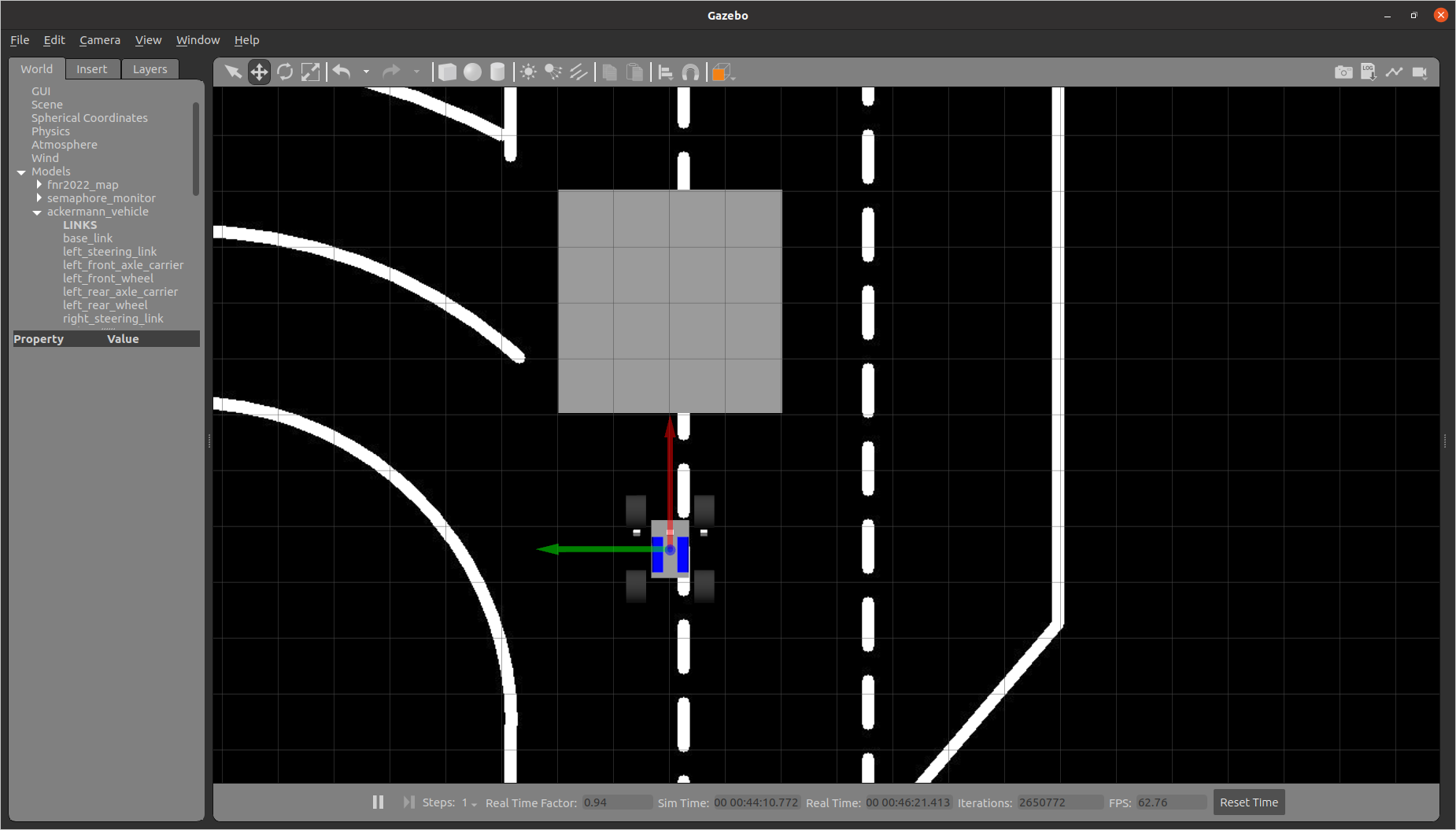
image 11

image 12
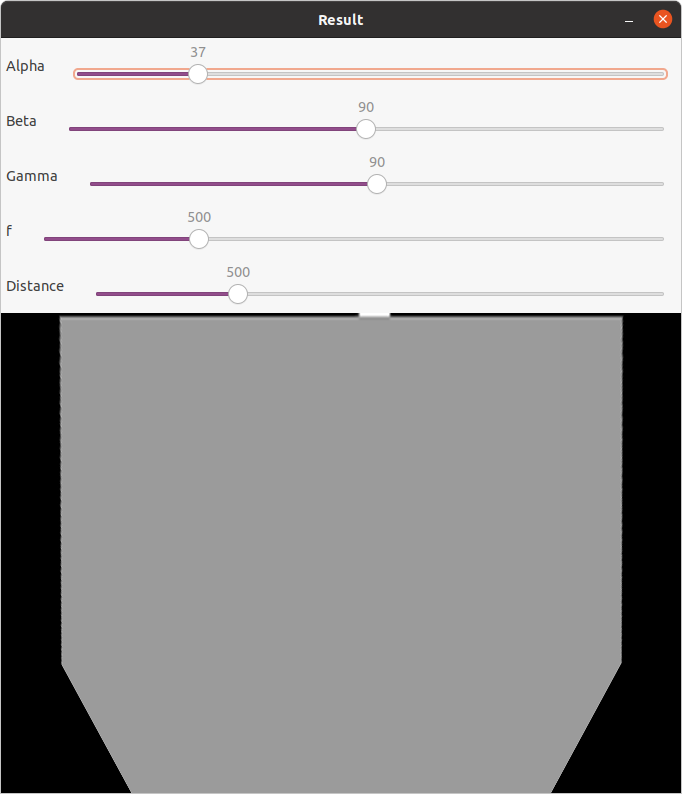
image 13
Após procurar ajustar a distância do quadrado à viatura, ficando conforme visível nas imagens 11, 12 e 13, conclui que sem mudar outros parâmetros era impossível visualizar o quadrado de 1 metro na sua totalidade, pelo que reduzi o tamanho para 50 cm.
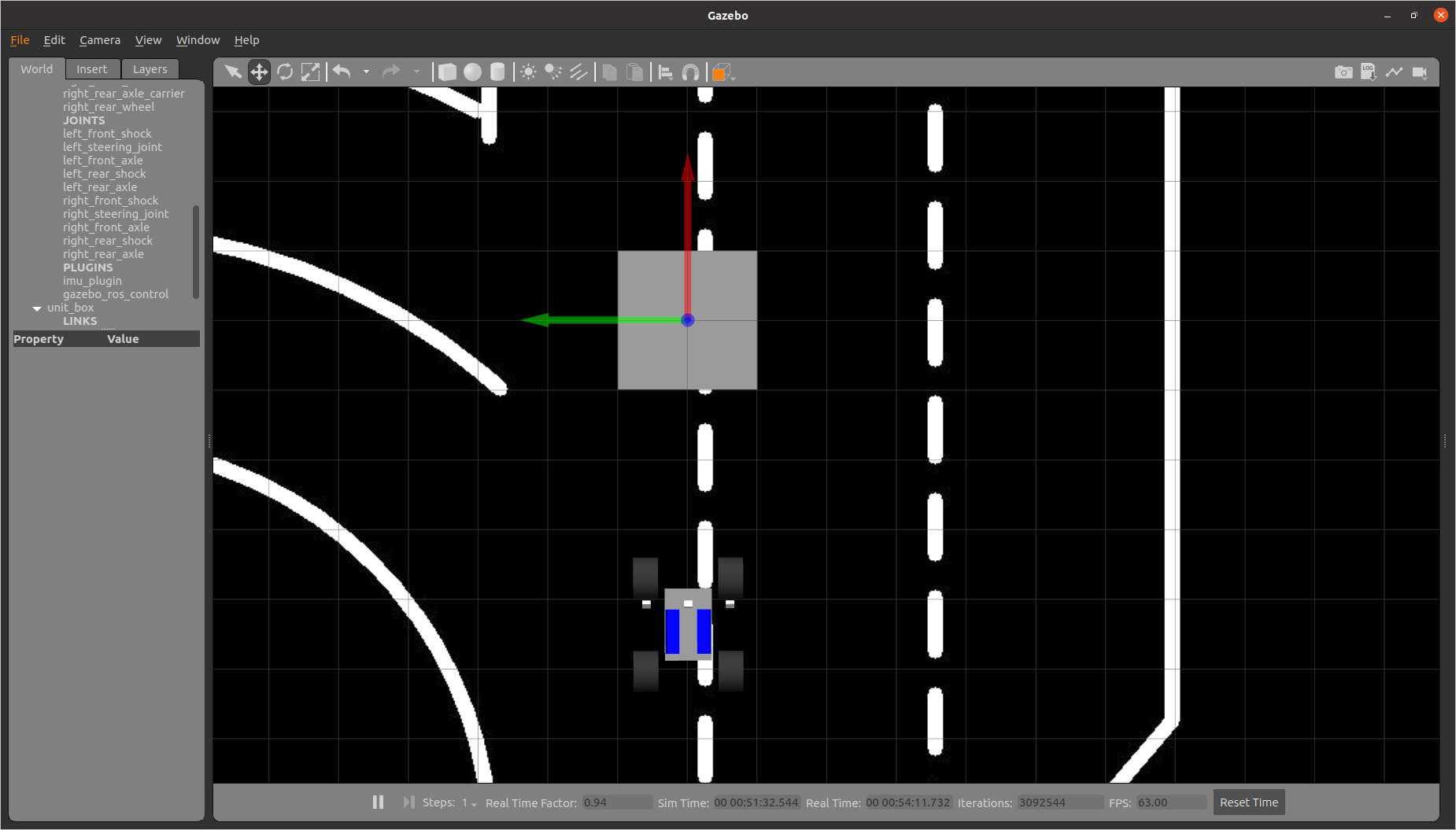
image 14

image 15
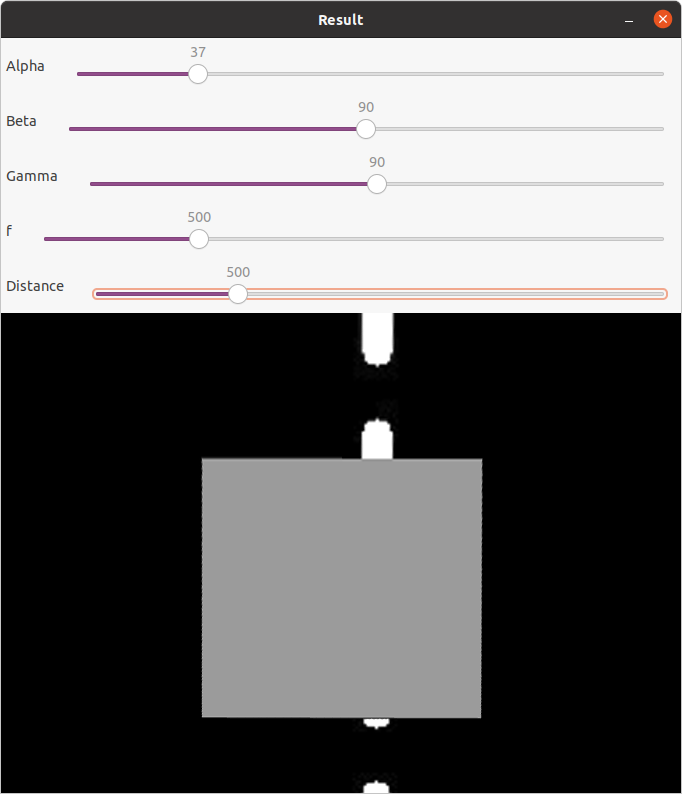 image 16
image 16
As imagens 14, 15 e 16, exibem, respectivamente, o ambiente no gazebo, a perspectiva da camera, e a perspectiva transformada.
Neste caso o quadrado é integralmente visível, no entanto, quando medido ao pormenor ele continua a estar comprimido na altura, já que o seu tamanho em pixels é de 279 x 259.
Aplicando ao programa1 os seguintes pontos:
source: [218, 191], [462, 191], [530, 374], [151, 374]
destination: [202, 145], [480, 145], [480, 404], [202, 404]
verificou-se que para a mesma imagem (imagem 15) correspondia uma imagem semelhante à da imagem 16.
Como a discrepância na dimensão dos pixels do quadrado é de 20 pixels, foi efectuada uma alteração na coordenada y dos dois primeiros pontos de destino. Globalmente ficou assim.
destination: [202, 125], [480, 125], [480, 404], [202, 404]
O resultado melhorou bastante, e o quadrado ficou com 279 x 279 px, pelo que também se pode concluir que nesta vista existem 558 pixels por metro.
Aplicando esta nova transformação a imagem 5, obteve-se então a seguinte imagem que está menos comprimida.

Conclusão, para obter empiricamente as coordenadas dos pontos dos quatro pontos na imagem de origem e respectivas as coordenadas dos pontos na imagem de destino, deve-se usar um quadrado de dimensões conhecidas que esteja inteiramente visível.
Referencias
https://theailearner.com/tag/cv2-warpperspective/
https://www.edmundoptics.com/knowledge-center/application-notes/imaging/understanding-focal-length-and-field-of-view/